Almost all electronic products need to use operational amplifier, operational amplifier (referred to as operational amplifier), its full English name is Operation Amplifier, abbreviated as OPAM, which is a high-gain voltage amplifier with DC coupling, differential mode input and usually single-ended output. Today, we'll give you some basic knowledge about operation.

Looking through all the books and courses of analog electronic technology, when introducing the operational amplifier circuit, it is nothing more than defining the circuit first. For example, this is a non-inverting amplifier, then deducing the relationship between its output and input, and then getting Vo=(1+Rf)Vi, which is an inverting amplifier, and then getting VO = 0-RF * VI. Finally, students often get the impression that it is enough to remember the formula! If we change the circuit a little, they won't find their way north! I have interviewed at least 100 candidates for electronics major with college degree or above. As a result, I can analyze the operational amplifier circuit given by me perfectly. There are no more than 10 candidates! It is conceivable that other majors graduated.

       Today, I'll teach you two invincible tricks. These two tricks are clearly written in all the teaching materials of operational amplifier circuits, namely "virtual short" and "virtual break". However, if you want to use them brilliantly, you must have a deep foundation.

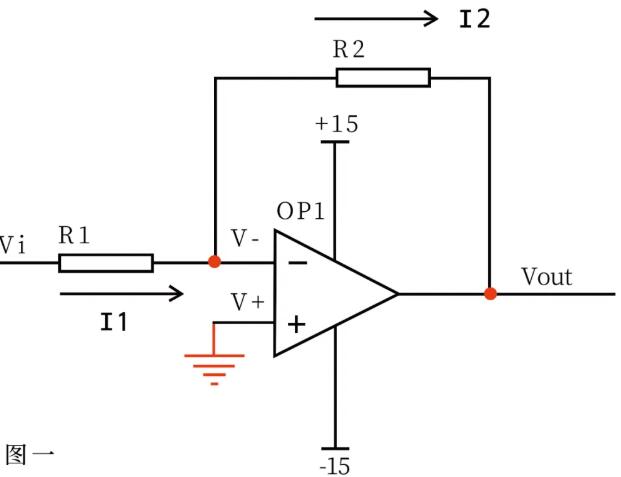
As shown in Figure 1, the non-inverting terminal of an operational amplifier is grounded =0V, and the inverting terminal and the non-inverting terminal are short, so it is also 0V. The input resistance of the inverting input terminal is very high, and there is almost no current injection or outflow. Then R1 and R2 are equivalent to series connection, and the current flowing through each component in a series circuit is the same, that is, the current flowing through R1 and R2 is the same. The current i1 flowing through R1 = (VI-V-)/R1 ... A the current I2 flowing through R2 = (V-VOUT)/R2 ... BV-= V+= 0 ... Ci1 = I2 ... D Vout = (-R2/R1)*Vi is obtained by solving the above junior middle school algebraic equation. This is the input-output relationship of the legendary reverse amplifier.

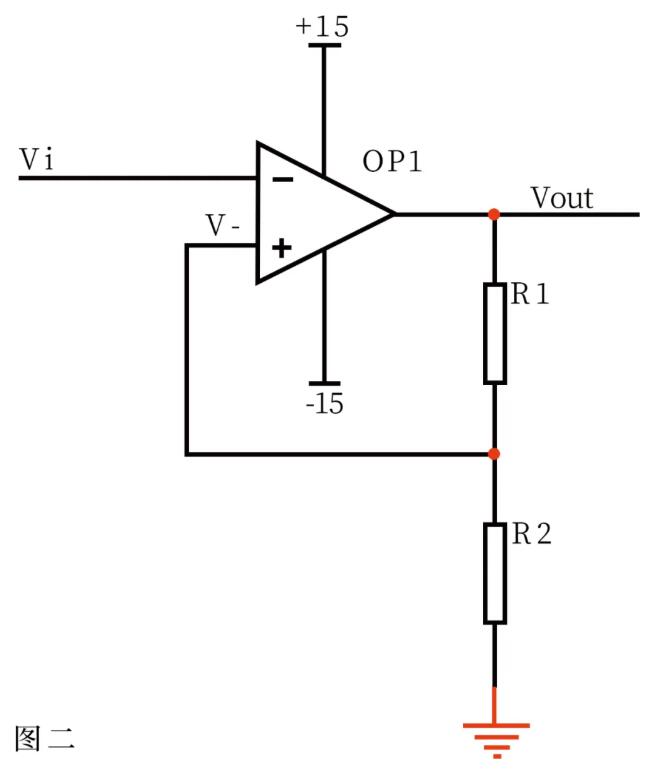
In Figure 2, Vi and V- are imaginary short, so Vi = V- a is imaginary. There is no current input and output at the reverse input terminal, and the current through R1 and R2 is equal. Let this current be I, which is obtained by Ohm's law: I = Vout/(R1+R2)  b ViEqual to the voltage division on R2, i.e. Vi = I*R2 ……c Vout=Vi*(R1+R2)/R2 is obtained by abc formula. This is the formula of the legendary non-inverting amplifier.

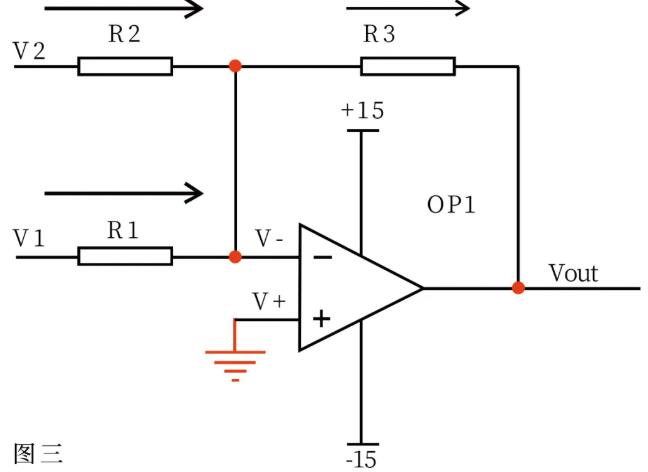
In Figure 3, it is known from imaginary short: V- = V+ = 0 ……a is known from imaginary break and Kirchhoff's law, and the sum of currents through R2 and R1 is equal to the current through R3, so (V1–V-)/R1+(V2–V-)/R2 = (V–VOUT)/R3 …… B is substituted into Formula A, and Formula B becomes

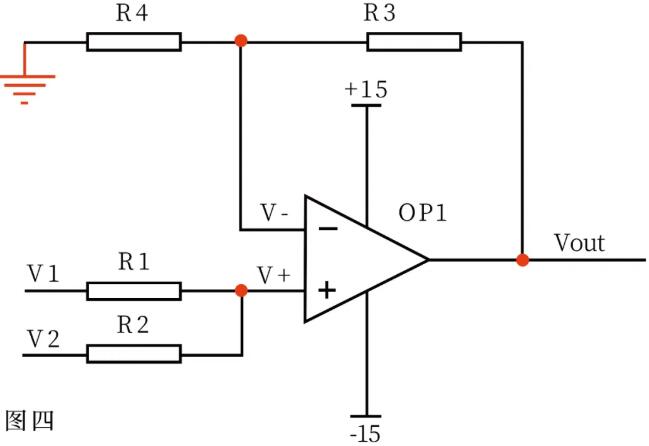
Please look at Figure 4. Because of the virtual break, no current flows through the non-inverting terminal of the operational amplifier, so the currents flowing through R1 and R2 are equal, and similarly, the currents flowing through R4 and R3 are equal. Therefore, (v1–v+)/R1 = (v+-v2)/R2 … A (vout–v-)/R3 = v-/R4 … B is known from the imaginary short: v+= v-… C If R1=R2 and R3=R4, then V+= (v1

Fig. 5 shows that the current through R1 is equal to the current through R2, and similarly, the current through R4 is equal to the current through R3, so there are (V2–V+)/R1 = V+/R2 … A (V1–V-)/R4 = (V-VOUT)/R3 … B If R1=R2, then V+= V2/2. Then v-= (vout+v1)/2 ... d is known from the imaginary short v+= v-... e so Vout=V2-V1. This is the legendary subtractor.

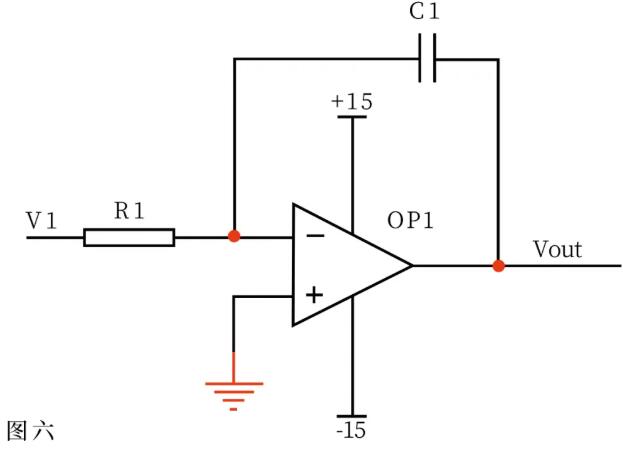
In the circuit shown in Figure 6, the voltage at the reverse input terminal is equal to that at the same direction terminal, and the current through R1 is equal to that through C1. The current I through R1 = v1/R1 and the current I through C1 = c * duc/dt =-c * dvout/dt, so the output voltage of Vout=((-1/(R1*C1))∫V1dt is proportional to the integration of the input voltage with time. This is the legendary integration circuit. If V1 is a constant voltage U, the above formula is transformed into Vout = -U*t/(R1*C1) t is time, and the output voltage of Vout is a straight line from 0 to negative power supply voltage.

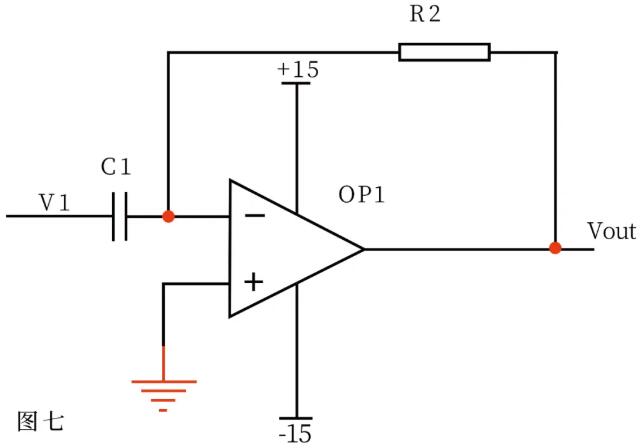
In Figure 7, the current through capacitor C1 and resistor R2 is equal, and the voltage at the same terminal and the reverse terminal of the operational amplifier is equal. Then: Vout = -i * R2 = -(R2*C1)dV1/dt This is a differential circuit. If V1 is a DC voltage added suddenly, the output Vout corresponds to a pulse with the opposite direction to V1.

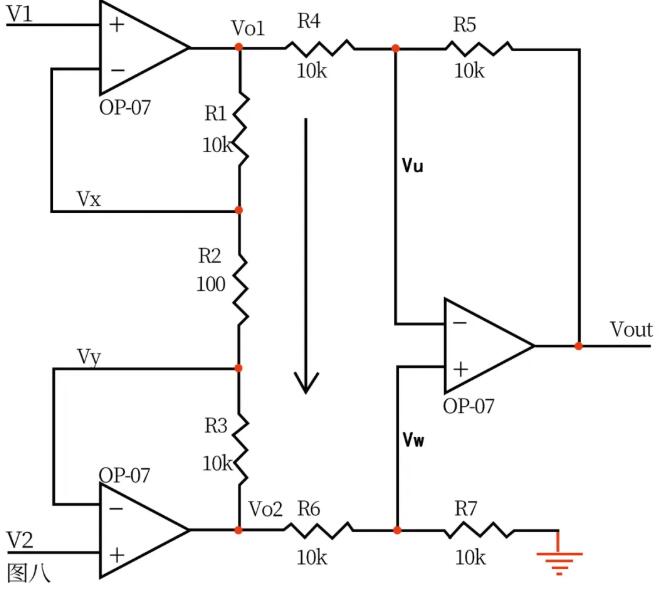
In Figure 8, Vx = V1 ……a Vy = V2 ……b is known by imaginary fault. If no current flows through the input of the operational amplifier, R1, R2 and R3 can be regarded as series connection, and the current through each resistor is the same. The current I = (VX-VY)/R2 ... C is: VO1-VO2 = I * (R1+R2+R3) = (VX-VY) (R1+R2+R3)/R2 ... D is known by imaginary fault, and the current flowing through R6 is equal to that flowing through R7. If R6=R7, VW = Then vout–vu = vu–vo1, so vu = (vout+vo1)/2 … f is known by imaginary short, Vu = Vw ……g is vout = VO2–vo1 of efg … h is vout = (Vy -Vx) (R1+R2+R3)/R2 of dh in the above formula (R1+) This circuit is the legendary differential amplifier circuit.

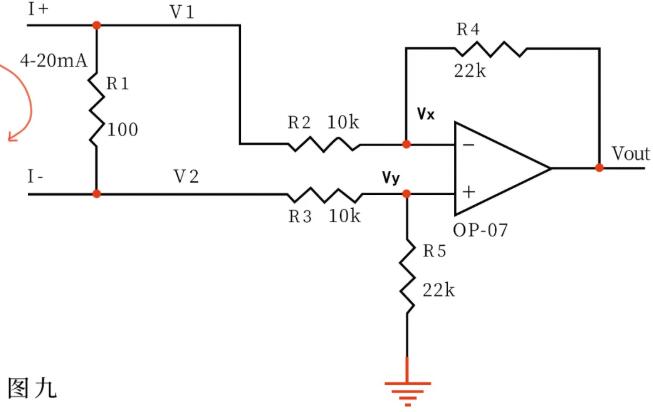
Analyze a circuit that everyone is exposed to more. Many controllers accept 0~20mA or 4~20mA current from various testing instruments. The circuit converts this current into voltage and then sends it to ADC for conversion into digital signal. Figure 9 is such a typical circuit. As shown in figure 4~20mA current flows through the sampling 100Ω resistor R1, and a voltage difference of 0.4~2V will be generated on R1. It is known from the supposition that if no current flows through the input of the operational amplifier, the currents flowing through R3 and R5 are equal, and the currents flowing through R2 and R4 are equal. Therefore: (V2-VY)/R3 = VY/R5 … A (V1-VX)/R2 = (VX-VOUT)/R4 … B: Vx = Vy ……c The current varies from 0 to 20 mA, Then v1 = v2+(0.4 ~ 2) ... d is obtained by substituting cd formula into B formula (v2+(0.4 ~ 2)-vy)/R2 = (vy-vout)/R4 ... e If R3=R2 and R4=R5, then Vout =-(0.4 ~ 2) is obtained by E-A. The formula f Vout = -(0.88~4.4)V, that is, 4~20mA current is converted into -0.88 ~ -4.4V voltage, which can be sent to ADC for processing.

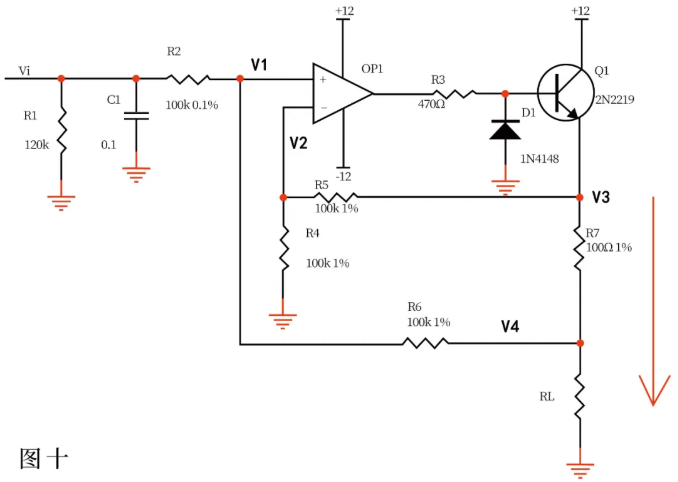
Current can be converted into voltage, and voltage can also be converted into current. Figure 10 is such a circuit. The negative feedback in the figure is not directly fed back through the resistor, but the emitter junction of transistor Q1 is connected in series. Don't think it is a comparator. As long as it is an amplifier circuit, the law of virtual short and virtual break is still in line!

It is known from the supposition that no current flows through the input of the operational amplifier.，

Then (VI–v1)/R2 = (v1–v4)/R6 … a
In the same way (v3–v2)/r5 = v2/R4 … b
Knowing v1 = v2 ... c by virtual short.
If R2=R6 and R4=R5, V3-V4=Vi by abc formula

The above formula shows that if the voltage across R7 is equal to the input voltage Vi, the current I through R7 = VI/R7, and if the load Rl < < 100 kω, the current through RL and R7 is basically the same.

Disclaimer: This article is reproduced from "Gu Taiwei". This article only represents the author's personal views, and does not represent the views of Sacco Wei and the industry. It is only for reprinting and sharing to support the protection of intellectual property rights. Please indicate the original source and author when reprinting. If there is any infringement, please contact us to delete it.

Company Tel: +86-0755-83044319
Fax/fax:+86-0755-83975897
Email: 1615456225@qq.com
QQ: 3518641314 Manager Li
QQ: 332496225 Manager Qiu
Address: Room 809, Block C, Zhantao Technology Building, No.1079 Minzhi Avenue, Longhua New District, Shenzhen